Ejercicio 6: Animación sobre una curva

El ejercicio

En este ejercicio, se requiere mostraran objeto no simétrico siguiendo una curva suavizada en la escena. Para realizar esto, se creara un objeto asimétrico a base de primitivas, se dibujara una curva de Bézier en la escena y por ultimo se animara el objeto siguiendo la curva a una velocidad determinada.

Creación del objeto

Inspirado en el clásico juego de Q*Bert. Se recreara el icónico escenario del juego: Una pirámide formada por distintos niveles de cubos.

Para esto, vamos a utilizar la librería de WebGL Fundamentals, Primitivas. La cual nos permite crear primitivas como cubos, esferas, conos, etc. Creamos los cubos y los organizamos en los distintos niveles, dibujando los vértices de los cubos de un color distinto en cada nivel. Obtenemos el siguiente resultado:

Sin embargo, esta forma sigue siendo simétrica en varios ejes. Por lo tanto, se eliminaran algunos cubos para eliminar la simetría. Nuestro resultado final se puede ver a continuación:

Creación de la curva

Utilizaremos una curva de Bézier cúbica. En esta se utilizan cuatro puntos, un punto de inicio, un punto final y dos puntos de control. La creación de la curva se hace a trabes de interpolaciones lineales entre los distintos puntos. A continuación mostrare una implementación de una curva de Bézier cúbica en Unity para exponer su creación.

Primero, se dibujan líneas del punto de inicio a el primer punto de control, desde el primer punto de control a el segundo, y del segundo al punto final.

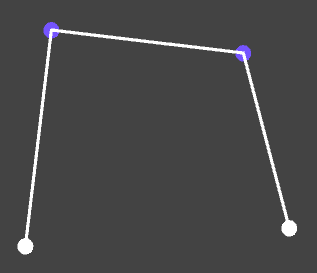
Se generan un punto en cada una de estas líneas, resultado de la interpolación de la posición entre cada uno de los puntos. Para t=0.65:

Posteriormente se generan líneas entre estos puntos:

Se repiten los pasos anteriores, generando puntos en las nuevas líneas y a su vez generando una línea entre estos puntos:

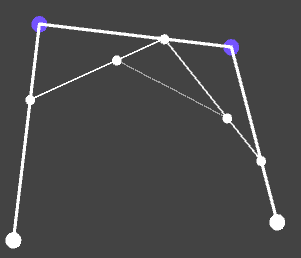
Por ultimo, se crea un nuevo punto dada la interpolación sobre esta ultima línea. La posición de este punto dictara la curva creada. Además, la ultima línea creada representa la tangente de la curva. Visto en movimiento:

Para la implementación en JavaScript, primero se creara una función que nos permita realizar la interpolación linear entre dos puntos:

function lerp(a, b, t) {
    var len = a.length;
    if(b.length != len) return;

    var x = [];
    for(var i = 0; i < len; i++)
        x.push(a[i] + t * (b[i] - a[i]));
    return x;
}

Esta función Serra utilizada para obtener el punto de la curva de Bézier:

function bezier(a, b, p1, p2, t) {
    var ap = lerp(a, p1);
    var pp = lerp(p1, p2);
    var pb = lerp(p2, b);

    var app = lerp(ap, pp);
    var ppb = lerp(pp, pb);

    return lerp(app, ppb);
  }

Por ultimo, vamos a dibujar la curva creada. Para esto debemos obtener un cierto numero de puntos dentro de la curva. Entre mas puntos obtengamos, mayor resolución tendrá su visualización. En este caso vamos a obtener 100 puntos:

  var points = [];
  var t = 0.0;
  while (t<=1.0) {
    var p = bezier(startP, endP, c1P, c2P, t);
    points.push(p);
    t += 0.01
  }

Con estos puntos, dibujamos en la escena en el modo de LINE_STRIP, de este modo se creara una curva en el espacio 3D.

Animación

Para crear la animación, primero modificamos la función de Bézier para que nos entregue tanto la posición como el punto donde el objeto debe mirar (la dirección tangente):

function bezier(a, b, p1, p2, t) {
    var ap = lerp(a, p1, t);
    var pp = lerp(p1, p2, t);
    var pb = lerp(p2, b, t);

    var app = lerp(ap, pp, t);
    var ppb = lerp(pp, pb, t);

    return {
      position: lerp(app, ppb, t),
      lookAt: ppb
    };
  }

Creamos unas series de variables globales que guarden el estado de la animación:

var t = 0; //Tiempo animación actual
var animacion = 5000; //Tiempo total de animacion
var tiempo = Date.now(); //Tiempo actual
var regreso = false; //Animacion de regreso

En el método de actualización, encontramos el factor de interpolación de la animación:

var tActual = Date.now();
var delta = tActual - tiempo;
tiempo = tActual;
t+= delta;
if (t>animacion) {
   t = 0;
   regreso = !regreso;
}
var interpolacion = t/animacion;
if(regreso) {
   interpolacion = 1 - interpolacion;
}

Se puede observar que la variable binaria de regreso la cambiamos cada vez que la animación termine, si esta es verdadera el factor de interpolación se invierte de manera que el programa realiza la animación en reversa.

Por ultimo, encontramos la posición en la curva y actualizamos el grafo de escena:

var bezierInfo = bezier(startP, endP, c1P, c2P, interpolacion);
m4.lookAt(bezierInfo.position, bezierInfo.lookAt, [0,1,0], root.localMatrix);
root.updateWorldMatrix();

Resultado final

El demo del ejercicio se puede ver en este fiddle.

Tiempo dedicado

Para este ejercicio, había planeado un tiempo de 4 horas. Sin embargo, se realizo en 5 horas, ya que se presentaron muchos problemas dibujando la curva en la escena.

Ejercicio 6