Tema de Profundización:
Uso artístico de Shaders
Para el tema de profundización, me interese en la creación de shaders con fines artísticos. Con esto me refiero a los shaders que no usan modelos de iluminación realista o comunes. En cambio, buscan crear un estilo específico que interprete la iluminación o de la escena de un modo particular para generar la imagen que se desee. Ejemplos de esto se pueden ver en diversos videojuegos con gráficos altamente estilizados, donde la iluminación afecta la escena de forma irrealista pero placentera a la vista. Uno de los juegos más conocidos que hacen uso de esta herramienta es The Legend of Zelda: Wind waker, donde hacen uso del llamado Cel Shading. Otro conocido ejemplo es el juego Okami, donde los desarrolladores crearon un Shader que dibuja la escena con un estilo que resembla el arte japonés de tinta china en papel.
Cabe mencionar que no en todos los casos los shaders buscan desviarse de la realidad, por el contrario, también se buscan desarrollar shaders para representar fenómenos físicos de la luz que con los modelos conocidos es imposible representar. Por ejemplo, los ejemplos de refracción de la luz a través del agua o de un vidrio, o la translucencia de algunos materiales como la piel humana. También se pueden encontrar ejemplos de shaders que modifican la geometría de ciertas formas, o que le dan propiedades especiales, por ejemplo la capacidad de replicar emisión de luz en algunos vértices de la geometría.
Para esta presentación, quiero analizar 3 ejemplos de shaders especiales realizados en WebGL, tratando de entender como se pudo lograr el resultado y posibles usos prácticos. Por último, ir más en profundidad en el último ejemplo de un Toon/Cel Shader, revisando el código del shader y viendo los pasos tomados para crearlo.
Ejemplo 1: Wireframe Shader

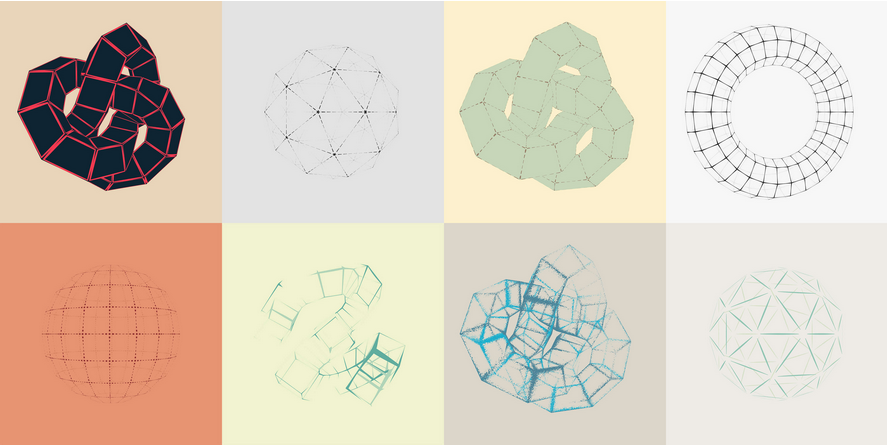
En este ejemplo, podemos ver un shader que busca crear una apariencia de Wireframe acentuando las aristas de la geometría. Este shader no maneja ningún tipo de iluminación, en cambio este cambia el color de los fragmentos entre los vértices de la geometría, revelando la estructura que esta tiene. El shader también acepta una gran cantidad de parámetros para modificar la forma en que acentúa las aristas, incluyendo el color, el grosor de las líneas, poder usar doble línea. También acepta parámetros para que no dibuje la figura sino solos sus vértices, o cosas mas avanzadas como el uso de funciones de ruido para animar el grosor y transparencia del acento.
Se podría utilizar este shader, de pronto agregándole la capacidad de aceptar iluminación, para generar elementos interesantes en juegos o en visualizaciones de algunos elementos.
Ejemplo 2: Efecto de Refracción
Otro ejemplo interesante que encontré fue este blog sobre la simulación de materiales refractivos en WebGL. En el explican distintos métodos como lograr el efecto y sus distintas limitaciones. Llegan a utilizar mapas precalculados de refracción, donde, para la geometría especifica, crean una textura en donde cada píxel guarde información sobre la distorsión generada por la refracción de la geometría en ese punto. Este método daba muy buenos resultados ya que el shader no debía realizar ningún calculo adicional, solo debía leer el mapa precalculado y realizar la distorsión acordemente.
En los ejemplos presentados, dibujaban la geometría sobre una imagen estática, según el mapa de refracción, usaban esta misma imagen distorsionada como textura de la geometría, dando la apariencia que la geometría es un cristal que esta distorsionando la imagen que pasa por ella. Este método era eficiente para el ejemplo, sin embargo, si se quiere que la geometría se mueva en una escena 3D, no seria tan sencillo. Se debería estar constantemente renderizando una imagen de lo que se encuentra detrás de la geometría refractiva para poder realizar el proceso.
Ejemplo 3: Toon/Cel Shader
Por ultimo, encontré este ejemplo, donde se demostraba el uso del reconocido Toon Shader o Cel Shader. Este shader busca darle una apariencia de caricatura a la geometría 3D, de forma que la imagen final simule un dibujo hecho en papel. Para esto, el shader crea un contorno negro sobre alrededor de la geometría y, a diferencia de shaders tradicionales, no realiza un difuminación suave de la luz sobre la superficie curva, en cambio crea una serie de niveles discretos donde la luz afecta distinto la superficie según su inclinación. Efectos de esta clase son muy utilizados en video juegos para conseguir ese estilo especifico, aparentando que el juego tiene complejas animaciones 2D cuando en realidad es una representación 3D.
Ya que es un efecto muy usado y no es complicado de replicar, fui mas a fondo para revisar el código del ejemplo y de este pen hecho por Thom Chiovoloni para replicar el efecto. El pen era muy interesante porque creaba dinámicamente una geometría compleja, muy apropiada para ver el efecto del Cel Shader.
Para empezar, borre el shader y lo cambie por un shader con iluminación tradicional:

Primero vamos a crear el contorno negro alrededor de la geometría. Para realizar esto se requiere realizar dos pasadas por cada fotograma. En la primera pasada dibujaremos la geometría totalmente negra con una leve expansión. En la segunda, dibujaremos la figura normalmente, de forma que queda dibujada encima de la anterior, y solo queda la expansión que realizamos, lo cual será nuestro contorno.
Para esto, creamos un shader especial para la primera pasada, en el vertex shader realizaremos la expansión de la geometría. Para esto, a la posición que recibimos como atributo le vamos a sumar la normal multiplicada por un pequeño offset. Lo que esto esta realizando es mover cada vértice de la geometría la distancia expresada por el offset en dirección de la normal asociada al vértice. Si las normales se encuentran definidas correctamente, esto es una expansión uniforme de la geometría.
attribute vec3 a_position;
attribute vec3 a_normal;
uniform mat4 u_projectionMat;
uniform mat4 u_modelviewMat;
void main() {
float offset = 0.01;
vec4 pos = vec4(a_position+(a_normal*offset), 1.0);
gl_Position = u_projectionMat * u_modelviewMat * pos;
}
En el fragment shader de esta primera pasada, pintamos todos los fragmentos de un mismo color, en este caso negro.
uniform vec4 u_color;
void main() {
gl_FragColor = u_color;
}
Ya que no estamos calculando iluminación, si vemos el resultado de la primera pasada parece una forma 2D completamente negra.

Sin embargo, al realizar la segunda pasada, dibujamos la geometría sin expansión encima y podemos apreciar el efecto del contorno.

Ahora vamos a replicar el efecto de Cel Shading, obteniendo los niveles discretos de iluminación en vez de una curva suave como la vemos anteriormente. Para esto modificamos el shader que se utiliza en la segunda pasada. El vertex shader no realiza nada especial esta vez, solo calcula la posición según la matriz de proyección y vista, y le envía al fragment shader el vector normal asociado.
attribute vec3 a_position;
attribute vec3 a_normal;
uniform mat4 u_projectionMat;
uniform mat4 u_modelviewMat;
uniform mat3 u_normalMat;
uniform vec3 u_diffuse;
varying vec3 v_eyeNormal;
void main() {
v_eyeNormal = u_normalMat * a_normal;
gl_Position = u_projectionMat * u_modelviewMat * vec4(a_position, 1.0);
}
En este momento, el fragment shader esta realizando el calculo de la iluminación como se realiza tradicionalmente. Calcula el producto punto entre la normal y la dirección de la luz, lo cual da un valor entre -1 y 1 que representa el coseno del ángulo entre ellas. Coge el máximo de este valor y 0, y este lo utiliza como factor de ponderación de la parte difusa de la luz en el calculo del color.
varying vec3 v_eyeNormal;
varying vec3 v_diffuse;
uniform vec3 u_light;
uniform vec3 u_ambient;
void main() {
vec3 en = normalize(v_eyeNormal);
vec3 ln = normalize(u_light);
float df = max(0.0, dot(en, ln));
vec3 color = u_ambient + df * v_diffuse;
gl_FragColor = vec4(color, 1.0);
}
Para realizar la división en niveles discretos crearemos una nueva función, el valor del producto punto lo recibiéremos como parámetro de la función. El resultado del producto punto lo multiplicamos por el numero de niveles que queremos que la geometría tenga, esto quiere decir que ahora el valor no va de 0 a 1, sino de 0 a el numero de niveles. Para saber en que nivel se encuentra este fragmento, utilizamos la función de piso, por lo tanto el nivel es un numero entero entre 0 y el numero de niveles menos 1. Por ultimo, necesitamos saber que tanto porcentaje de la luz cada nivel aumenta, para esto dividimos 1 que seria el total entre el numero de niveles (en algunos casos esto resulta en una imagen algo oscura, por lo que aumentamos este valor realizando 1 sobre el numero de niveles menos 0.5). Por ultimo, devolvemos este valor por el numero del nivel donde se encuentra el fragmento.
float celShade(float d) {
d *= u_celShading;
float nivel = floor(d);
float perc = 1.0 / (u_celShading - 0.5);
return nivel * perc;
}
Para conseguir el resultado final, simplemente modificamos la función main para que utilice la función que creamos anteriormente.
void main() {
vec3 en = normalize(v_eyeNormal);
vec3 ln = normalize(u_light);
float df = max(0.0, dot(en, ln));
float cdf = celShade(df);
vec3 color = u_ambient + cdf * v_diffuse;
gl_FragColor = vec4(color, 1.0);
}
Y obtenemos nuestra imagen final, con el contorno y los niveles discretos de iluminación.
En el ejemplo original, Thom realiza una serie de pasos adicionales para mejorar la imagen. Primero, crea pequeños niveles intermedios para que las divisiones entre la iluminación no sean tan bruscas, lo cual podría verse como un estilo de anti-aliasing. También agrega luz especular al modelo con un parámetro de shininess.